7.5 - Rotating a Camera

Tilt Motion¶

To tilt a camera means you rotate a camera’s orientation around its u axis. You can tilt up (positive rotation) or tilt down (negative rotation).

As in the previous lesson, there are two basic ways to implement a tilt camera motion:

Modify the parameters of a call to the lookat function and then call lookat to create a camera transformation matrix, or
Directly modify the definition of a camera’s position and coordinate axes.

Let’s solve the problem both ways.

Use `lookAt` to Tilt¶

In the previous lesson you studied a class called LookAtCamera which defines a camera using two points and one vector: 1) the location of the camera, 2) the location of a point along it’s line-of-sight, and 3) a direction that is upwards. To “tilt” a camera, we add a new function to the LookAtCamera class called tilt.

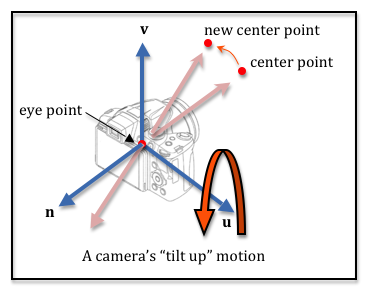
A tilt movement must change the center point. We need to rotate the location of the center point about the camera’s u axis, which will change the line-of-sight of the camera. Remember that the camera will be invalid if the line-of-sight and the “up vector” are pointing in the same direction. Therefore, if the angle between the line-of-sight vector and the “up vector” gets small, we need to rotate the “up_vector” to keep it away from the line-of-sight vector. The diagram illustrates a tilt movement.

The tilt function receives an angle in degrees which is the amount of rotation. If the angle is positive, the function will “tilt up”. If the angle is negative, the function will “tilt down”. The basic steps are:

Calculate the camera’s u axis.
Move the camera to the origin. This moves the eye point to the origin and it moves the center point to some location relative to the origin. You translate by (-eye_x, -eye_y, -eye_z). This is required because all rotation is about the origin.
Rotate the center point about the u axis by the angle of tilt.
Move the camera back to its original location. You translate the center point by (eye_x, eye_y, eye_z).
Use the lookAt function to recalculate the camera’s transformation matrix.

Note that all of the above operations need to be performed by 4-by-4 transformation matrices because you are not necessarily working in a plane that is parallel to the global axes.

Use the following demo to experiment with tilting a camera. Notice that tilting is always relative to the camera’s frame of reference. The code is editable if you want to experiment with the code.

Show: Code Canvas Run Info

lookat_camera.js

/**
 * lookat_camera.js, By Wayne Brown, Spring 2016
 */

/**
 * The MIT License (MIT)
 *
 * Copyright (c) 2015 C. Wayne Brown
 *
 * Permission is hereby granted, free of charge, to any person obtaining a copy
 * of this software and associated documentation files (the "Software"), to deal
 * in the Software without restriction, including without limitation the rights
 * to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
 * copies of the Software, and to permit persons to whom the Software is
 * furnished to do so, subject to the following conditions:
 *
 * The above copyright notice and this permission notice shall be included in all
 * copies or substantial portions of the Software.

* THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
 * IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
 * FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
 * AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
 * LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
 * OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
 * SOFTWARE.
 */

"use strict";
var Learn_webgl_matrix, Learn_webgl_vector3, Learn_webgl_point3;

//-----------------------------------------------------------------------
/**
 * Store and manipulate a camera based on the parameters of the lookAt function.
 * @constructor
 */
window.LookAtCamera = function () {

// Constructor
  var self = this;

// Objects needed for internal elements and calculations
  var matrix = new Learn_webgl_matrix();
  var V = new Learn_webgl_vector3();
  var P = new Learn_webgl_point3();

// Camera definition at the default camera location and orientation
  self.eye       = P.create(0, 0, 0);  // (x,y,z), origin
  self.center    = P.create(0, 0, -1); // (x,y,z), down -Z axis
  self.up_vector = V.create(0, 1, 0);  // <dx,dy,dz>, up Y axis

// Create a matrix to hold the camera's matrix transform
  self.transform = matrix.create();

// Scratch objects for calculations
  var u, n, new_center, tilt_rotate;
  u = V.create();  // u coordinate axis of camera
  n = V.create();  // n coordinate axis of camera
  new_center = P.create();
  tilt_rotate = new matrix.create();

//-----------------------------------------------------------------------
  /**
   * Using the current values for eye, center, and up, calculate a new
   * camera transformation matrix.
   */
  self.updateTransform = function () {
    // Calculate a new camera transform
    matrix.lookAt(self.transform,
                  self.eye[0], self.eye[1], self.eye[2],
                  self.center[0], self.center[1], self.center[2],
                  self.up_vector[0], self.up_vector[1], self.up_vector[2]);
  };

//-----------------------------------------------------------------------
  /**
   * Perform a tilt operation on a camera
   * @param angle Number The angle of rotation about the u axis.
   */
  self.tilt = function (angle) {
    // Calculate the n camera axis
    V.subtract(n, self.eye, self.center);  // n = eye - center
    V.normalize(n);

// Calculate the u camera axis
    V.crossProduct(u, self.up_vector, n);
    V.normalize(u);

// Move the camera coordinate system to the origin. We only calculate
    // the center point because we are not going to change the eye point
    P.subtractVector(new_center, self.center, self.eye);

// Create a rotation transform about u
    matrix.rotate(tilt_rotate, angle, u[0], u[1], u[2]);

// Rotate the center point. Since this is a vector that has no location,
    // we only need to multiply by the rotation part of the transform.
    matrix.multiplyV3(new_center, tilt_rotate, new_center);

// Translate the center point back to the location of the camera.
    P.addVector(self.center, new_center, self.eye);

// If the angle between the line-of-sight and the "up vector" is less
    // than 10 degrees or greater than 170 degrees, then rotate the
    // "up_vector" about the u axis.
    // cos(10 degrees) = 0.985; cos(170 degrees) = -0.985
    if (Math.abs(V.dotProduct(n, self.up_vector)) >= 0.985) {
      matrix.multiplyV3(self.up_vector, tilt_rotate, self.up_vector);
    }
    // Calculate a new camera transform
    self.updateTransform();
  };

//-----------------------------------------------------------------------
  /**
   * Perform a truck operation on the camera
   * @param distance Number How far to move the camera
   */
  self.truck = function (distance) {
    // Calculate the n camera axis
    V.subtract(n, self.eye, self.center);  // n = eye - center
    V.normalize(n);

// Calculate the u camera axis
    V.crossProduct(u, self.up_vector, n);
    V.normalize(u);

// Scale the u axis to the desired distance to move
    V.scale(u, u, distance);

// Add the direction vector to both the eye and center positions
    P.addVector(self.eye, self.eye, u);
    P.addVector(self.center, self.center, u);

self.updateTransform();
  };

self.updateTransform();
};

To investigate camera tilt motion:

Manipulate the parameters of a lookAt() created virtual camera to position and orient a camera.
Push the tilt button below to "tilt" from the camera's current position and orientation.

The left canvas shows the relative location of the scene objects and the camera. The right canvas shows the scene from the camera's vantage point.

Manipulate the function lookAt(M, eye_x, eye_y, eye_z, center_x, center_y, center_z, up_dx, up_dy, up_dz)

eye (0.0, 0.0, 5.0)	center (0.0, 0.0, 0.0)	up <0.0, 1.0, 0.0>
X: -5.0 +5.0	X: -5.0 +5.0	X: -1.0 +1.0
Y: -5.0 +5.0	Y: -5.0 +5.0	Y: -1.0 +1.0
Z: -5.0 +5.0	Z: -5.0 +5.0	Z: -1.0 +1.0

Each click of the tilt button rotates 1 degree about the u axis.

Shader errors, Shader warnings, Javascript info

Open this webgl program in a new tab or window

You must study the above code carefully to understand camera movement. Please read the code comments as you study the statements.

Modify A Camera’s Definition¶

Let’s implement the “tilt” motion of a camera using the camera’s basic definition: a location and three coordinate axes. Using the AxesCamera class we introduced in the previous lesson, we add a new function called tilt. To tilt a camera we simply need to rotate the v and n coordinate axes about the u axis. The eye location of the camera does not change.

Please study the tilt function in the following demo program. This demo code is editable.

Show: Code Canvas Run Info

axes_camera.js

/**
 * lookat_camera.js, By Wayne Brown, Spring 2016
 */

/**
 * The MIT License (MIT)
 *
 * Copyright (c) 2015 C. Wayne Brown
 *
 * Permission is hereby granted, free of charge, to any person obtaining a copy
 * of this software and associated documentation files (the "Software"), to deal
 * in the Software without restriction, including without limitation the rights
 * to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
 * copies of the Software, and to permit persons to whom the Software is
 * furnished to do so, subject to the following conditions:
 *
 * The above copyright notice and this permission notice shall be included in all
 * copies or substantial portions of the Software.

* THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
 * IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
 * FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
 * AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
 * LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
 * OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
 * SOFTWARE.
 */

"use strict";
var Learn_webgl_matrix, Learn_webgl_vector3, Learn_webgl_point3;

//-----------------------------------------------------------------------
/**
 * Store and manipulate a camera based on its location and its
 * local coordinate system.
 * @constructor
 */
window.AxesCamera = function () {

// Constructor
  var self = this;

// Objects needed for internal elements and calculations
  var matrix = new Learn_webgl_matrix();
  var V = new Learn_webgl_vector3();
  var P = new Learn_webgl_point3();

// Camera definition at the default camera location and orientation.
  self.eye = P.create(0, 0, 0);  // (x,y,z), origin
  self.u   = V.create(1, 0, 0);  // <dx,dy,dz>, +X axis
  self.v   = V.create(0, 1, 0);  // <dx,dy,dz>, +Y axis
  self.n   = V.create(0, 0, 1);  // <dx,dy,dz>, +Z axis

// Create a matrix to hold the camera's matrix transform
  self.transform = matrix.create();

// Scratch objects for calculations
  var u_scaled, rotate;
  u_scaled = V.create();  // a scaled u coordinate axis of camera
  rotate = matrix.create();

//-----------------------------------------------------------------------
  /**
   * Using the current values for eye, u, v, and n, set a new camera
   * transformation matrix.
   */
  self.updateTransform = function () {
    var tx = -V.dotProduct(self.u, self.eye);
    var ty = -V.dotProduct(self.v, self.eye);
    var tz = -V.dotProduct(self.n, self.eye);

// Use an alias for self.transform to simplify the assignment statements
    var M = self.transform;

// Set the camera matrix
    M[0] = self.u[0];  M[4] = self.u[1];  M[8]  = self.u[2];  M[12] = tx;
    M[1] = self.v[0];  M[5] = self.v[1];  M[9]  = self.v[2];  M[13] = ty;
    M[2] = self.n[0];  M[6] = self.n[1];  M[10] = self.n[2];  M[14] = tz;
    M[3] = 0;          M[7] = 0;          M[11] = 0;          M[15] = 1;
  };

//-----------------------------------------------------------------------
  /**
   * Update the camera's transformation matrix for a tilt motion.
   * @param angle
   */
  self.tilt = function (angle) {
    // Rotate the camera's coordinate system about u; updates v and n
    matrix.rotate(rotate, angle, self.u[0], self.u[1], self.u[2]);
    matrix.multiplyV3(self.v, rotate, self.v);
    matrix.multiplyV3(self.n, rotate, self.n);

// Use an alias for self.transform to simplify the assignment statements
    var M = self.transform;

// Update the 2nd and 3rd row of the camera transformation because only
    // the v and n axes changed.
    M[1] = self.v[0];  M[5] = self.v[1];  M[9]  = self.v[2];
    M[2] = self.n[0];  M[6] = self.n[1];  M[10] = self.n[2];

// Update the translate values of ty and tz
    M[13] = -V.dotProduct(self.v, self.eye);
    M[14] = -V.dotProduct(self.n, self.eye);
  };

//-----------------------------------------------------------------------
  /**
   * Perform a "truck" operation on the camera
   * @param distance
   */
  self.truck = function (distance) {
    // Scale the u axis to the desired distance to move
    V.scale(u_scaled, self.u, distance);

// Add the direction vector to the eye position.
    P.addVector(self.eye, self.eye, u_scaled);

// Set the camera transformation. Since the only change is in location,
    // change only the values in the 4th column.
    self.transform[12] = -V.dotProduct(self.u, self.eye);
    self.transform[13] = -V.dotProduct(self.v, self.eye);
    self.transform[14] = -V.dotProduct(self.n, self.eye);
  };

self.updateTransform();
}

To investigate camera tilting motion:

Manipulate the position and orientation of a camera.
Push the tilt button below to "tilt" from the camera's current position and orientation.

The left canvas shows the relative location of the scene objects and the camera. The right canvas shows the scene from the camera's vantage point.

Manipulate the camera's position and orientation:

eye (0.0, 0.0, 5.0)		angle = 0.0
X: -5.0 +5.0	Rotate about the camera's u axis:
Y: -5.0 +5.0	Rotate about the camera's v axis:	-180.0 +180.0
Z: -5.0 +5.0	Rotate about the camera's n axis:

Each click of the tilt button rotates 1 degree about the u axis.

Shader errors, Shader warnings, Javascript info

Open this webgl program in a new tab or window

Summary¶

A camera movement that involves rotation will rotate about one of the current axes of the camera’s coordinate system. If a camera tilts, the rotation is about the u axis. If a camera pans, the rotation is about the v axis. If a camera cants, the rotation is about the n axis. Camera motion is almost always about the camera’s current frame of reference.

As in the previous lesson, manipulating the actual camera definition (a point and 3 axes) requires less computation but more mathematical understanding of the camera matrix transform.

Glossary¶

tilt camera: Rotate a camera upwards or downwards, keeping its location unchanged.
pan camera: Rotate a camera left or right, keeping its location unchanged.
cant camera: Rotate a camera about its line-of-sight, keeping its location unchanged.

7.5 - Rotating a Camera¶

Tilt Motion¶

Use lookAt to Tilt¶

Modify A Camera’s Definition¶

Summary¶

Glossary¶

Use `lookAt` to Tilt¶