9.1 - Introduction to Lighting¶

A Review of Light Properties¶

Please re-read lesson 3.8 - Light Modeling.

Did you really re-read lesson 3.8. If not, please read it now. It’s important!

Types of Light Sources¶

There are many different sources of light. Four commonly used models to describe light sources are:

• Point light source: The light is inside the scene at a specific location and it shines light equally in all directions. An example is be a table lamp. Point light sources are modeled using a single location, (x,y,z,1).
• Sun light source: The light is outside the scene and far enough away that all rays of light are basically from the same direction. An example is the sun in an outdoor scene. Sun light sources are modeled as a single vector, <dx, dy, dz, 0>, which defines the direction of the light rays.
• Spotlight light source: The light is focused and forms a cone-shaped envelop as it projects out from the light source. An example is a spotlight in a theatre. Spotlights are modeled as a location, (x,y,z,1), a direction, <dx.dy,dz,0>, a cone angle, and an exponent that defines the density of light inside the spotlight cone.
• Area light source: The light source comes from a rectangular area and projects light from one side of the rectangle. An example is a florescent light fixture in a ceiling panel. Area light sources are modeled as a rectangle, (4 vertices), and a direction, <dx.dy,dz,0>.

All of these models have one common attribute: the direction light is traveling. In the following lessons we will discuss how the direction of light is used to calculate the color of individual pixels on a face.

Color of Light¶

Light from a table lamp or the sun it typically a shade of white. However, some sources of light are not white, such as a red stop light, a blue neon sign, or a purple spotlight at a sporting event. When we model a light source, we specify its color using an RGB color value. If a light source gives off white light, we model its color as (1.0, 1.0, 1.0). If the light source gives off red light, we model its color as (1.0, 0.0, 0,0).

When you see a red object, you are seeing the red component of reflected light off of the surface of the object; the green and blue components of the light were absorbed by the object’s surface. A red object absorbs all wavelengths of light except the red wavelengths. This fact means that if you shine a blue light on a red object, you see black! All of the blue light is absorbed by the object’s surface. The interaction between the color of an object and the light reflected from its surface is an important visual effect we will model.

Calculating Light Reflection¶

To calculate light reflection, we need to have the position and orientation of three things:

• the object being rendered,
• the light source, and
• the camera.

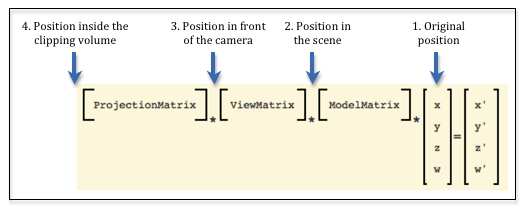
A scene rendering has one camera, one or more light sources, and one or more objects. The data required to render an object is stored in GPU buffer objects. The data needed for the camera and lights must be copied to the GPU before rendering begins. We would like to make the setup and initialization for rendering as efficient as possible. Consider the three fundamental transformations done on the vertices of a model, which are shown in the diagram below.

Let’s consider which object geometry values could be used for lighting calculations.

1. The original position: This is the original definition of the object. It does not represent the object’s position or orientation for a particular scene. We can’t use these values for lighting calculations.
2. Position in the scene: This is the position and orientation of an object after being transformed by the model transform. This places the object’s location and orientation relative to the other objects in the scene. Assuming that we know the location and orientation of the light sources and the camera, we could perform accurate light reflection calculations using these values.
3. Position in front of the camera: This is the position and orientation of an object after being transformed by the view transform. This retains the relative location and orientation of objects in a scene. Assuming that we know the location and orientation of the light sources, we could perform accurate light reflection calculations using these values. Notice that for these geometric values, the camera is located at the origin with its local coordinate system aligned to the global coordinate system. This has the advantage that we don’t have to send the camera’s location and orientation to the shader programs because we know exactly where the camera is.
4. Position inside the clipping volume: The geometric values have been transformed by the projection transform and are ready for clipping. The meaning of the x and y values have been de-coupled from the z values of each geometric vertex. The vertices no longer have their same relative relationship with other 3D positions in the scene. (Remember, the perspective transform did a non-linear mapping of the z values into the clipping volume.) We can’t use these values for accurate lighting calculations.

Therefore, we have two possible “3D spaces” in which to perform accurate lighting calculations. The “camera space” has a clear advantage because the camera is in a known location and orientation and we don’t have to transfer its position and orientation to the GPU shader programs. And the fact that the camera is locationed at the global origin simplifies some of the light reflection calculations.

To make all of this work you have to create two separate transformation matrices in your JavaScript program and pass both of them to your shader programs. This transformation matrix:

will perform all of the transformations required for the graphics pipeline, while this transformation matrix will produce valid locations and orientations for lighting calculations.

Lighting Algorithm¶

To render a scene that uses lighting calculations to color pixels, we perform the following algorithm:

1. In your JavaScript program:
   1. Use a model and camera transformation to get the light source into its correct position and orientation.
   2. Transfer the light source’s position and orientation to the GPU’s shader programs
   3. Create an additional transformation matrix that includes the desired projection matrix.
   4. Transfer two transformation matrices to the GPU’s shader programs; one for lighting calculations, another for rendering calculations.
2. In your GPU shader program:
   1. Assume the camera is at the global origin looking down the -Z axis.
   2. Use the light source data and the model data to calculate light reflection.
   3. Assign a color to a pixel based on the light reflection.

Lesson Organization¶

The following lessons on lighting describe how to implement point light sources and follow this general outline:

• Introduce a “lighting model.”
• Explain the math needed to calculate the “lighting model.”
• Provide a WebGL demo program that implements the “lighting model”. It is very important that you experiment with the demo program to understand the visual effects of the “lighting model”.
• Explain the details for the shader programs that implement the “lighting model.”

If you understand how to implement lighting for point light sources, you should be able to extend these ideas to other types of lights, such as sun, spotlights, and area lights.

The details can be overwhelming, so please take your time and master each lighting model before moving on the next, more complex lighting model.

Glossary¶

light source

Where light in a scene comes from.

light model

A set of data and algorithms that simulates a light source and how it interacts with objects in a scene.